Answer:
The load varies jointly as the width w, the square of the depth d, and inversely as the length l, this can be represented below as
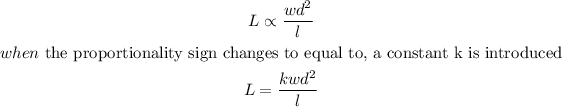
From the question, the given values are
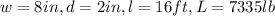
By substituting the values, we will have
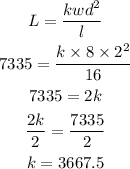
Substitute the value of k to get the equation connecting the w,d,l and L
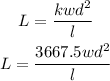
To get the value of the load, we will substitute the value of
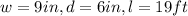
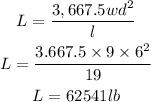
Hence,
The final answer is =62541 lb