Question

Determine the common ration of a geometric progresión if the first termis -8 and the 6th term is -1/4.

Answer 1

1/2

Step-by-step explanation:

Given a geometric progression with the following:

• The first term, a= -8

,

• The 6th term = -1/4

The nth term of a geometric progression is obtained using the formula:

`\begin{gathered} U_n=ar^(n-1)\text{ where:} \\ a=\text{first term} \\ r=\text{common ratio} \end{gathered}`

Substitute the given values:

`U_6=(-8)* r^(6-1)=-(1)/(4)`

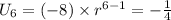
We solve the equation for r:

`\begin{gathered} -8r^5=-(1)/(4) \\ \text{Divide both sides by -8} \\ (-8r^5)/(-8)=-(1)/(4*-8) \\ r^5=(1)/(32) \end{gathered}`

Next, take the 5th root of both sides:

`\begin{gathered} \sqrt[5]{r^5}=\sqrt[5]{(1)/(32)} \\ r=(1)/(2) \end{gathered}`

The common ratio of the geometric progression is 1/2.