Question

Hi, I was doing some homework and got stuck on these two questions.

Answer 1

In the quadratic equation

`y=ax^2+bx+c`

We can find the nature of its roots by using the discriminant

`\Delta=b^2-4ac`

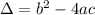
We have 3 cases

`\begin{gathered} b^2-4ac>0\rightarrow2\text{ real roots} \\ b^2-4ac=0\rightarrow1\text{ real root} \\ b^2-4ac<0\rightarrow No\text{ real roots (imaginary roots)} \end{gathered}`

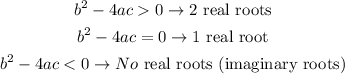
#a)

For the quadratic equation

`y=-2x^2+16x-35`

a = -2

b = 16

c = -35

Let us find the discriminant to find the nature of the roots

`\begin{gathered} \Delta=(16)^2-4(-2)(-35) \\ \Delta=256-280 \\ \Delta=-24 \end{gathered}`

Since the value is negative, then we will use the 3rd case above

The equation has NO Real roots

The quadratic function has NO real roots, it will have imaginary roots

#b

For the quadratic equation

`y=9x^2+kx+16`

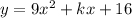
Since it has only one x-intercept

That means it has only ONE real root

Then we will use the 2nd case above

`b^2-4ac=0`

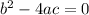
Since:

a = 9

b = k

c = 16

Then

`\begin{gathered} k^2-4(9)(16)=0 \\ k^2-576=0 \end{gathered}`

Add 576 to each side

`\begin{gathered} k^2-576+576=0+576 \\ k^2=576 \end{gathered}`

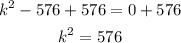
Take a square root for each side

`\begin{gathered} \sqrt[]{k^2}=\pm\sqrt[]{576} \\ k=\pm24 \end{gathered}`

The values of k are -24 and 24