Question

Solve the following problem using elimination...systems of lincar equations. 2. Rafael, an exchange student from Brazil, made phone calls within Canada, to the United States, and to Brazil. The rates per minute for these calls vary for the different countries. Use the information in the following table to determine the rates. (No Calculator) Month September October November Time within Canada (min) 90 70 50 Time to the U.S. (min) 120 100 110 Time to Brazil (min) 180 120 150 Charges (S) $252.00 $184.00 $206.00 Express the problem as a system of linear equations: Solve the system of linear equations to determine the unit cost of each item.

Answer 1

Let's call X the unit cost to the calls within Canada, Y the unit cost to the calls to U.S., and Z the unit cost to the calls to Brazil.

Based on the table we can formulate the following equations:

90X + 120Y + 180Z = 252

70X + 100Y + 120Z = 184

50X + 110Y + 150Z = 206

Then, to use the elimination method we need to multiply one equation by a number an add it to a second equation, so:

`\begin{gathered} 90X+120Y+180Z=252 \\ (-2)/(3)(90X+120Y+180Z)=252\cdot((-2)/(3)) \\ -60X-80Y-120Z=-168 \end{gathered}`

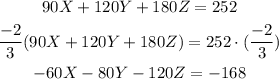
Then, adding this equation to the second one, we get:

-60X - 80Y - 120Z = -168

70X + 100Y + 120Z = 184

10X + 20 Y = 16

Repeating the process with the first and third equation:

`\begin{gathered} (-5)/(6)(90X+120Y+180Z)=252\cdot((-5)/(6)) \\ -75X-100Y-150Z=-210 \end{gathered}`

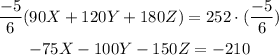
So:

- 75X - 100Y - 150Z = -210

50X + 110Y + 150Z = 206

-25X + 10Y = -4

Now, we can multiply the last equation by -2, adding with the previous one and solve for X as:

(-25X + 10Y)*(-2) = -4(-2)

50X - 20Y = 8

Then:

50X - 20Y = 8

10X + 20 Y = 16

60X = 24

X = 24/60

X = 2/5

Therefore, we can replace X by 2/5 and solve for Y as:

50X - 20Y = 8

50*(2/5) - 20Y = 8

20 - 20Y = 8

-20Y = 8 - 20

-20Y = - 12

Y = (-12)/(-20)

Y = 3/5

Finally, replacing X by 2/5 and Y by 3/5, we get that Z is equal to:

90X + 120Y + 180Z = 252

90*(2/5) + 120*(3/5) + 180Z = 252

36 + 72 +180Z = 252

108 + 180Z = 252

180Z = 252 - 108

180Z = 144

Z = 144/180

Z = 4/5

The unit cost to canada is Canada $0.4, to U.S. is $0.6, and to Brazil is $0.8

Answers: X = 2/5 = 0.4

Y = 3/5 = 0.6

Z = 4/5 = 0.8