Given a line made by two points (x1, y1) and (x2, y2), its slope (m) is computed as:
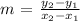
In this case, the points are (-2, -1) and (1, 8). The slope is:

Two lines are perpendicular if the multiplication of their slopes is equal to -1. Then:
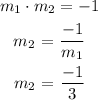
Isolating y in option D:
2x = -6y +3
2x - 3 = -6y
2/(-6)x - 3/(-6) = y
-1/3x + 1/2 = y
where -1/3 is its slope. Then, this line is perpendicular to line segment AB