Answer:
x = 1
Explanation:
1. Expand the expression:
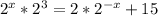
2. Evaluate the power:
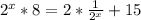
3. Substitute. Let's use t for
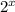 :
:
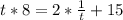
4. Solve for t :
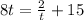
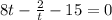
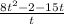
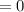
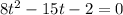

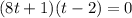
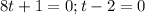

5. Substitute back:
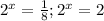
6. Solve for x
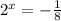 is false for any value of x because the exponential function is always positive, so there is no real solution.
is false for any value of x because the exponential function is always positive, so there is no real solution.
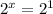 since the bases are the same, set the exponents equal
since the bases are the same, set the exponents equal
x = 1