SOLUTION
Step 1 :
In this question, we are meant to calculate the average rate of the change over the
interval

Step 2 :
For the average rate of change, we need to do the following calculations:
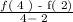
putting x = 4 in
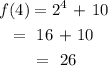
putting x = 2 in
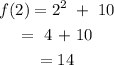
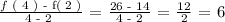
CONCLUSION: The average rate of change = 6.