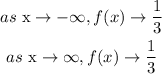29. Given
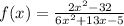
The end behavior of the function is the behavior of the graph of f(x) as x approaches positive infinity or negative infinity.
- For local behavior of the function, see the graph of the function:
As it can be seen that the graph is moving towards positive infinity as x --> -5/2 + and x ---> 1/3 -
And towards negative infinity as x --> -5/2 - and x --> 1/3 +
Thus the local behavior of the function is:
Answer
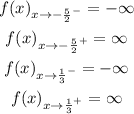
- For the end behavior of the function:
In words, we could say that as x values approach infinity, the function values approach y = 1/3 and as x values approach negative infinity, the function values approach y = 1/3. We can describe the end behavior symbolically by writing:
Answer