Question

An electronic store receives a shipment of 40 graphing calculators including eight that are defective four of the calculators are selected to be sent to a local high school how many of these selections will contain no defective calculators?

Answer 1

Given:

There are 40 graphing calculators.

8 out of 40 are defective.

4 calculators are randomly chosen.

To find:

The number of possible selections will contain no defective.

Step-by-step explanation:

The number of non-defective calculators is,

`40-8=32`

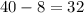
The possible number of ways of selecting 4 calculators from 32 non-defective calculators is,

`\begin{gathered} ^(32)C_4=(32!)/((32-4)!4!) \\ =(32!)/(28!4!) \\ =(28!*29*30*31*32)/(28!*4*3*2*1) \\ =29*5*31*8 \\ =35960 \end{gathered}`

Final answer:

The number of possible selections will be 35960.