Compound Interest
The final value of an investment of P dollars for t years at an interest rate of r is given by:
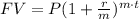
Where m is the number of compounding periods per year.
(a)
Lori buys a CD for P = $1500 that earns r = 6% = 0.06 interest compounded monthly for t = 10 years. Here m = 12 because there are 12 months in a year.
Substituting:
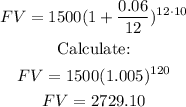
The CD will be worth $2729.10 in 10 years.
(b) If the interest compounds daily, then m = 360. Calculating:
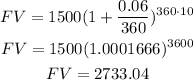
The CD will be worth $2733.04 in 10 years.
(c) For t = 5 years:
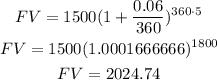
The CD will be worth $2024.74 in 5 years.