ANSWER
32.8 m/s
Step-by-step explanation
Given:
• The initial elevation of the sled, h = 55.0 m
,
• There is no friction
Find:
• The speed of the sled at the bottom of the hill, v
By the Law of Conservation of Energy, since there is no friction,
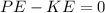
Therefore,
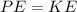
The expressions for the gravitational potential energy, PE, and the kinetic energy, KE, are,

We have to find v, so solving the equation above for v,
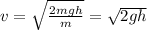
As we can see, it does not depend on the mass of the sliding object. Replace the known values and solve,
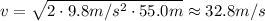
Hence, the speed of the sled at the bottom of the hill is 32.8 m/s, rounded to the nearest tenth.