a)
If we consider i pointing to west-east direction and j pointing to south-north direction, since the airspeed is 600 miles per hour headed to north, the jet velocity relative to the air is given by:
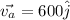
Since the jet stream is is 110 miles per hour in the northeasterly direction, we have:
![\begin{gathered} \vec{v_w}=110\cdot(\cos 45\degree\hat{i}+\sin 45\degree\hat{j}) \\ \vec{v_w}=55\sqrt[]{2}\hat{i}+55\sqrt[]{2}\hat{j} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/j220cbnrss5sk71zpapyx8t4k26qk9xb6x.png)
b)
The velocity of the jet relative to the ground is given by:
![\begin{gathered} \vec{v_a}+\vec{v_w}=_{}55\sqrt[]{2}\hat{i}+(600+55\sqrt[]{2})\hat{j} \\ \vec{v_a}+\vec{v_w}=55\sqrt[]{2}\hat{i}+5(120+11\sqrt[]{2})\hat{j} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/xp71vi7evjp53ajcp8mq0j0i7f8pjpgm3y.png)
c)
Then, the actual speed of the jet relative to the ground is given by:
![\sqrt[]{\lbrack(55\sqrt[]{2})^2+(600+55\sqrt[]{2})^2}=\sqrt[]{372100+66000\sqrt[]{2}}=10\sqrt[]{3721+660\sqrt[]{2}}](https://img.qammunity.org/2023/formulas/mathematics/college/gjbeysxfzhuspsuknq1e7gp5ykemeeia0o.png)
Finally, the direction of the jet relative to the ground is given by:
![\tan ^(-1)\frac{600+55\sqrt[]{2}}{55\sqrt[]{2}}=\tan ^(-1)((60)/(11)\sqrt[]{2}+1)](https://img.qammunity.org/2023/formulas/mathematics/college/ojubfs1jbn7rodgqmsvs41gi2zfqukv8uk.png)