Question

which table of values satisfied the linear equation Y=-3/4X-6X. Y-8. 120. -68. -12X. Y-4. -90. -64. -3X. Y-4. -30. -64. -9X. Y-8. -120. -68. 0

Answer 1

Given linear function is:

`y=-(3)/(4)x-6`

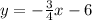
From the given options, let us check the value of y by substituting given value of x

Let x=-8

we get,

`y=-(3)/(4)(-8)-6`
`\begin{gathered} y=6-6=0 \\ y=0 \end{gathered}`

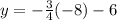
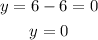
we get y=0, Hence the first and last table has differenct value for y, B oth are not the required table for the given equation

Let x=-4, we get

`y=-(3)/(4)(-4)-6`
`\begin{gathered} y=3-6 \\ y=-3 \end{gathered}`

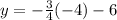
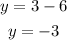
we get y=-3, third table satisfies the condition.

Let us check the values of y by using remaining x values.

Let x=0,

we get,

`y=-6`

This also satisfied, then let x=4

we get,

`y=-(3)/(4)(4)-6`
`\begin{gathered} y=-3-6 \\ y=-9 \end{gathered}`

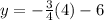
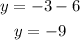
This is also satisfied,

Hence the required table for the given linear equation is,

X. Y

-4. -3

0. -6

4. -9