Given the arithmetic series below
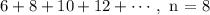
To find the sum of the arithmetic series,
We find the last term, i.e 8th term of the series
The formula to find the last term/formula for the arithmetic progression is given below
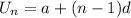
The common difference, d, is
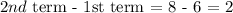
Where,
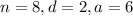
Substitute the values into the formula to find the 8th term
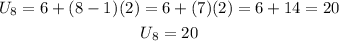
The formula to find the arithmetic series is

Where
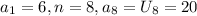
Subtsitute the values into the formula to find the arithmetic series above
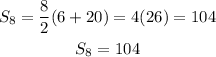
Hence, the sum of the arithmetic series is 104