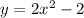Given:-
A set of data.
To find the required equation.
So from the given equation, the equation which suits is,
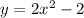
So now we prove it by substituting the values from the table.
When x=-2 we get the value as,
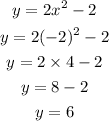
So the value of y is 6.
When x=-1. we get,
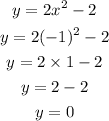
So the value of y is 0.
When x=0. we get,
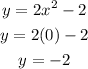
So the value of y is -2.
When x=1. we get,
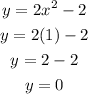
So the value of y is 0.
When x=2. we get,
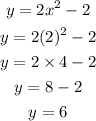
So the value of y is 6.
When x=3. we get,
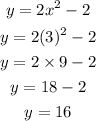
So the value of y is 16.
When x=4. we get,
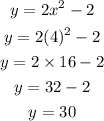
So the value of y is 30.
So from this we can conclude that the correct equation is,