Question

A bag contains 120 marbles. Some are red and the rest are black. There are 19 red marbles for every black marble How many red marbles are in the bag? red marbles b. Explain your reasoning. Type your response in the space below.

Answer 1

In this case, we have that there are 19 red marbles for every black marble:

19 red marble/ 1 black marble.

If we sum the red marbles and the black marbles, and we form the fraction to represent the totals, we have that:

`(19r)/(1b)\Rightarrow19+1=20\Rightarrow R=(19)/(20),B=(1)/(20)`

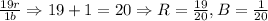
Then, we have that the red marbles are 19/20 of the total, and the black marbles are 1/20 of the total.

Therefore, to have a total of red marbles, we have that:

`R=(19)/(20)\cdot120m\Rightarrow R=(19\cdot120m)/(20)\Rightarrow R=114`

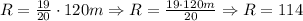
To check this result, we have that the black marbles are:

`B=(1)/(20)\cdot120m\Rightarrow B=6`

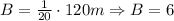
Then, if we divide the total of red marbles by the total of black marbles, we have:

`(114r)/(6b)=19=(19r)/(1b)`

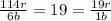
Thus, we confirm that we have 19 red marbles for every black marble.

Then, the total of red marbles is 114 red marbles.

You have 19 red marbles for every 1 black marble, then we have 19+1 = 20. Then, you form the fractions 19/20 and 1/20 to have the ratio of the total of red and black marbles. The fraction of the total of red marbles is 19/20, and the fraction of the total of black marbles is 1/20.