Question

Write the equation of the line passing through point (4, -2) and perpendicular to y = 4x + 2

Answer 1

In our case, we can note that the slope m is the coefficient of the variable x, that is,

`m=4`

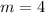
A perpendicular line must have a negative reciprocal slope, that is,

`\begin{gathered} M=-(1)/(m) \\ then \\ M=-(1)/(4) \end{gathered}`

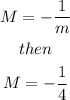
then, the searched line has the form

`y=-(1)/(4)x+b`

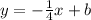
Now, we can find b by means of the given point (4,-2). Then, by replacing this point into the last equation, we get

`-2=-(1)/(4)(4)+b`

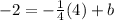
which gives

`-2=-1+b`

and by moving -1 to the left hand side, we have

`\begin{gathered} -2+1=b \\ -1=b \\ or\text{ quivalently,} \\ b=-1 \end{gathered}`

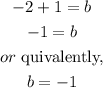
Therefore, the perpendicular line is

`y=-(1)/(4)x-1`

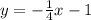
which corresponds to option b