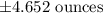Answer:
The margin of error associated with the true population mean is;
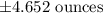
Step-by-step explanation:
Given the sample size as;

standard deviation as;
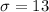
the mean;
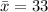
And confidence interval of 95%;
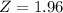
The Margin of Error MOE, can be calculated using the formula;
![\text{MOE}=\pm Z*\frac{\sigma}{\sqrt[]{n}}](https://img.qammunity.org/2023/formulas/mathematics/college/eh7txcjnzvie2949p4cg5tiyqcgc9tue4s.png)
Substituting the given values;
![\text{MOE}=\pm1.96*\frac{13}{\sqrt[]{30}}=\pm4.652](https://img.qammunity.org/2023/formulas/mathematics/college/ujngybe3hffr5e4g3ct4k78rz2z24bo596.png)
Therefore, the margin of error associated with the true population mean is;