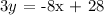The equation of the line through the given points is;
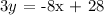
Here, we want to get the equation of the line that passes through the given points
Generally, we have the equation of a line as;
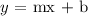
where m represents the slope and b represents the y-intercept
To find the slope, we use the slope formula which is as follows;
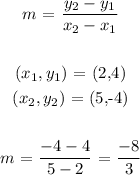
Partially, we have the complete equation as;
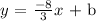
To get b, we use any of the points
Let us use the first point
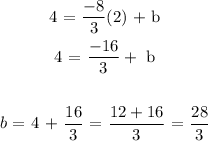
So, the equation of the line is;

Multiply through by 3, we have;