Question

Write a polynomial function with zeros at 3 & 2i, and passing through (4, 10). Give the value of the leading coefficient, a.

Answer 1

We know that the polynomial have zeros at 3 and 2i; now since it has an imaginary zero this means that its conjugate is also a zero, that is, -2i has to be a zero as well. We know that a polynomial function with zeros a, b and c can be express as:

`f(x)=A(x-a)(x-b)(x-c)`

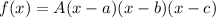
where A is some constant determine by some other conditions.

In this case the polynomial will have the form:

`f(x)=A(x-2i)(x+2i)(x-3)=A(x^2+4)(x-3)`

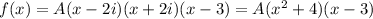
Now, to determine the value of A we use the fact that the polynomial passes through the point (4,10); this means that when x=4 the function has to be equal to 10, then we have:

`\begin{gathered} A(4^2+4)(4-3)=10 \\ A(20)(1)=10 \\ 20A=10 \\ A=(10)/(20) \\ A=(1)/(2) \end{gathered}`

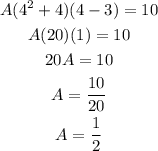
Therefore the function we are looking for is:

`f(x)=(1)/(2)(x^2+4)(x-3)`

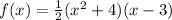
To find the leading coefficient we expand the expression, then we have:

`\begin{gathered} f(x)=(1)/(2)(x^3-3x^2+4x-12) \\ =(1)/(2)x^3-(3)/(2)x^2+2x-6 \end{gathered}`

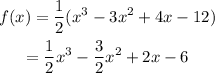
Therefore the leading coefficient of the function is equal to 1/2