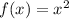The parent function can be determined by direct substitution of the x values in the table into the expressions of each function. Otherwise, we could also just plot the points given in the table on a graph and observe the form of the graph, and this will help us choose the right option.
By Substitution method:
a) Given that f(x) = x^2
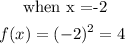
This tallies with the y value in the table.
Again:
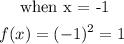
Since the y values tally with that given in the table, we can conclude that the parent function is f(x) = x^2
b) Given that f(x) = 2^x

This does not tally with the y value in the table
c) Given that f(x) = |x|

This does not tally with the y value in the table
d) Given that f(x) = x
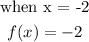
This also does not tally with the y value in the table
By Graphical method:
A plot of the values given in the table gives the following graph:
The above graph shows a parabola, which is obtained from quadratic functions.
Again, this points us to the conclusion that the parent function is f(x) = x^2
Thus, the answer is: option A