The given polynomial is
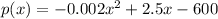
Differentiate with respect to x, we get
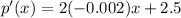
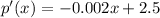
Equate this to zero, we get
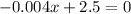
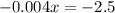
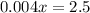
multiply by 1000 on both sides, we get
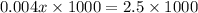
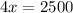
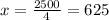
Hence they must sell 625 patterns to attain maximum profit.
Substitute x=625 in the given equation p(x), we get
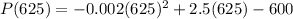
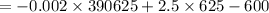
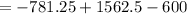
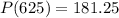
Hence the maximum profit is $ 181.25.