First, we need to find the z-score usign the next formula
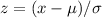
x is the score
μ is the mean
σ is the standard deviation
In our case
The mean (μ) = 4
The standard division (σ )= 1
The calls lasted less than (x)=3
we substitute the values

the with tables we can find the probability for the value of z given
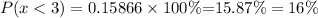
percentage of the calls that lasted less than 3 min is 15.87% approximately 16%