Given the parabola;
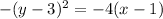
To pick the right statement we must compare it, with the right pattern of a parabola.
In this case, we would compare it with;
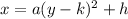
We can clearly see that the question can be simplified to look like the parabola above;
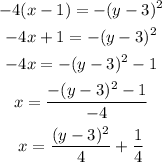
By comparing we can see that;
From the expression above we must note the following;
1)The value of "a" is positive
2)The variable "y" would be squared.
Hence, if "a" is positive and "y" is squared, the parabola would open up to the right and would also be horizontal.
This can be seen in the graph below;
Therefore, the right answer would be;
Answer: Option A