The dice has 6 faces numbered 1 to 6.
The probability of landing any number is 1/6.
The expected value is the sum of products of the probability and the winnings/losings.
So the expected value in this case is given by:
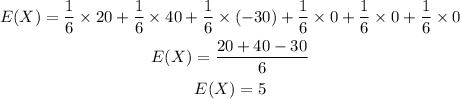
So the player can expect to win $5 per game in the long run.
Option C is correct.