Question

Find [a * b] for the following pairs of vectors

Answer 1

We have to calculate the a x b for the following vectors.

We will have the following vector as result of a x b:

`a* b=\begin{bmatrix}i & j & k \\ a_x & a_y & a_z \\ b_x & b_y & b_z \\ \end{bmatrix}=(a_y\cdot b_z-a_z\cdot b_y)\cdot i+(a_z\cdot b_x-a_x\cdot b_z)\cdot j+(a_x\cdot b_y-a_y\cdot b_x)\cdot k`

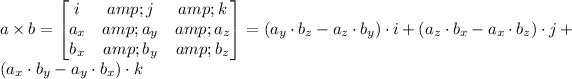
The resulting vector will be perpendicular to both a and b.

i) If a = (0,7,0) and b = (2,-4,7), we can calculate c as:

`\begin{gathered} c=a* b \\ c=(a_y\cdot b_z-a_z\cdot b_y)\cdot i+(a_z\cdot b_x-a_x\cdot b_z)\cdot j+(a_x\cdot b_y-a_y\cdot b_x)\cdot k \\ c=(7\cdot7-0\cdot(-4))\cdot i+(0\cdot2-0\cdot7)\cdot j+(0\cdot(-4)-7\cdot2)\cdot k \\ c=49\cdot i+0\cdot j+(-14)\cdot k \\ c=(49,0,-14) \end{gathered}`

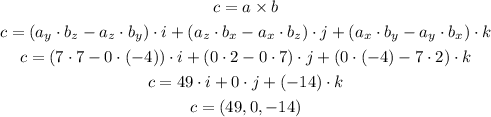
ii) If a = 4*i+7*k = (4, 0, 7) and b = -6*i + 2*j = (-6, 2, 0), then c will be:

`\begin{gathered} c=a* b \\ c=(a_y\cdot b_z-a_z\cdot b_y)\cdot i+(a_z\cdot b_x-a_x\cdot b_z)\cdot j+(a_x\cdot b_y-a_y\cdot b_x)\cdot k \\ c=(0\cdot0-7\cdot2)\cdot i+(7\cdot(-6)-4\cdot0)\cdot j+(4\cdot2-0\cdot(-6))\cdot k \\ c=-14i-42j+8k \\ c=(-14,-42,8) \end{gathered}`

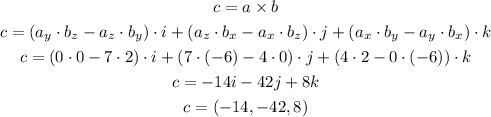
Answer:

i) c = 49i - 14k = (49,0,-14)

ii) c = - 14i - 42j + 8k = (-14, -42, 8)

[Note: you can express it either way, you have to pick one option to input the answer]