Question

Find the Y-coordinate of point P that lies 1/3 along segment RS, where R (-7, -2) and S (2, 4).

Answer 1

Given that the point P lies 1/3 along the segment RS as shown below:

To find the y coordinate of the point P, since the point P lies on 1/3 along the segment RS, we have

`\begin{gathered} RP:PS \\ \Rightarrow(1)/(3):(2)/(3) \\ thus,\text{ we have} \\ 1:2 \end{gathered}`

Using the section formula expressed as

`[(mx_2+nx_1)/(m+n),(my_2+ny_1)/(m+n)]`

In this case,

`\begin{gathered} m=1 \\ n=2 \end{gathered}`

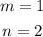
where

`\begin{gathered} x_1=-7 \\ y_1=-2 \\ x_2=2 \\ y_2=4 \end{gathered}`

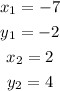
Thus, by substitution, we have

`\begin{gathered} [(1(2)+2(-7))/(1+2),(1(4)+2(-2))/(1+2)] \\ \Rightarrow[(2-14)/(3),(4-4)/(3)] \\ =[-4,\text{ 0\rbrack} \end{gathered}`

Hence, the y-coordinate of the point P is

`0`