The initial amount he deposited is 649.67
Step-by-step explanation:
time = t = 3 years
rate = r = 7% = 0.07
n = number of times it was compounded
n = quarterly = 4
The current balance = A = 800
P = in
amount deposited
We apply the compound interest formula to get the amount deposited:
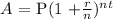
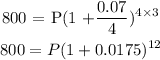

The initial amount he deposited is 649.67