The experiment is that 3 coins are tossed.
The event H is "all heads".
The event K is "at least one head".
We have to calculate the probability of H given K, that is: that we get 3 heads given that we have at least one head.
Then, one of the coins is already "fixed" as head. We are left with all the other possible combinations of the other 2 coins.
P(K) is the probability of having at least one head in the set.
We can list all the possible outcomes and see which one correspond to a K event.
HHH, HHT, HTH, HTT, THH, THT, TTH, and TTT.
Of the 8 possible outcomes, 7 are K events.
It was easier to think what outcome is not a K event, and that is that all coins are tail.
Then, P(K) = 7/8
The events that are both K and H are 1, and that is HHH. Then, P(H)=1/8.
The event H is included in the event K, so P(H)=P(H and K)=1/8
So we can write:
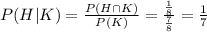
The conditional probabilty of H given K (the probability of three heads, given that we have already one head) is 1/7.