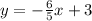Answer (assuming it can be in slope-intercept form):
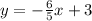
Explanation:
1) First, use the slope formula
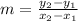 to find the slope of the line. Substitute the x and y values of the given points into the formula and solve:
to find the slope of the line. Substitute the x and y values of the given points into the formula and solve:
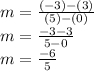
So, the slope is
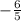 .
.
2) Now, use the slope-intercept formula
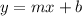 to write the equation of the line in slope-intercept form. All you need to do is substitute real values for the
to write the equation of the line in slope-intercept form. All you need to do is substitute real values for the
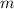 and
and
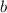 in the formula.
in the formula.
Since
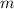 represents the slope, substitute
represents the slope, substitute
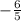 for it. Since
for it. Since
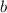 represents the y-intercept, substitute 3 for it. (Remember, the y-intercept is the point at which the line hits the y-axis. All points on the y-axis have an x-value of 0. Notice how the given point (0,3) has an x-value, too, so it must be the line's y-intercept.) This gives the following equation and answer:
represents the y-intercept, substitute 3 for it. (Remember, the y-intercept is the point at which the line hits the y-axis. All points on the y-axis have an x-value of 0. Notice how the given point (0,3) has an x-value, too, so it must be the line's y-intercept.) This gives the following equation and answer: