Question

Help me pleaseeeeeeeeeeeeee!!!!

Answer 1

The shorter leg measures 2.4 ft.

the longer leg measures 4.4 ft.

Explanation:

Let the shorter leg have length a and the longer leg have length b.

The hypotenuse has length c.

a² + b² = c²

a² + (a + 2)² = 5²

a² + a² + 4a + 4 = 25

2a² + 4a - 21 = 0

This is not factorable, so we use the quadratic formula.

Switch the variable to x. Now x is the length of the shorter leg.

2x² + 4x - 21 = 0

`x = (-b \pm √(b^2 - 4ac))/(2a)`

`x = (-4 \pm √(4^2 - 4(2)(-21)))/(2(2))`

`x = (-4 \pm √(16 + 168))/(4)`

`x = (-4 \pm √(184))/(4)`

`x = (-4 \pm 2 √(46))/(4)`

`x = (-2 \pm √(46))/(2)`

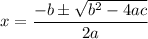
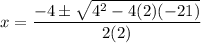
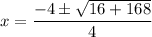
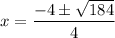
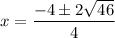
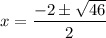
We discard the negative solution since the length of a side of a triangle cannot be negative.

`x = (-2 + √(46))/(2)`

`x = 2.391`

`x + 2 = 2.391 + 2 = 4.391`

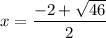
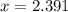
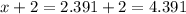
The shorter leg measures 2.4 ft.

the longer leg measures 4.4 ft.