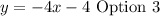The equation of the line given is,
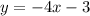
We were told that a line is parallel to the equation.
Therefore, from the equation above, the slope of the line is
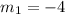
Rule for paralel line
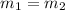
Hence, the slope (m2) is
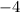
Also, the line passes through the point (-2,4).
The formula to calculate the equation in sope-intercept dform is,
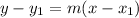
where,
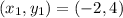
Therefore,
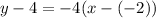
Simplify
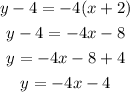
Hence, the equation of theline is