Question

50 points, please answer honestly.

Write and solve an equation to find the value of x so that the figures have the same area.
​

Answer 1

GIVEN THE FIGURES MUST HAVE THE SAME AREA

NOTE THE FIRST SHAPE IS A TRIANGLE WITH

b WHICH IS THE BASE WITH MAGNITUDE 8

AND THE h WHICH IS THE HEIGHT WITH MAGNITUDE (X+4)

WE KNOW THAT THE FORMULA TO CALCULATE THE AREA OF A TRIANGLE IS GIVEN BY

`= (1)/(2) * b * h`

SUBSTITUTE THE GIVEN VALUES IN THE FORMULA EQUATION AND SIMPLIFY TO GET THE EXACT EQUATION THAT REPRESENTS THE AREA OF THE TRIANGLE.

`a (triangle)= (1)/(2) (8)(x + 4) \\ a(triangle) = 4(x + 4) \\ a(triangle) = 4x + 16`

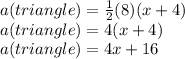
NOW LET US FOCUS ON THE AREA OF A RECTANGLE GIVEN BY FORMULA A=l×b

where l which is the length is given by (x+6) and The breadtg is given by 3

THEREFORE THE AREA OF THE RECTANGLE IS

`a(rectangle) = (x + 6)(3) \\ a(rectangle) = 3x + 18`

NOW EQUATE THE AREA OF THE TRIANGLE WITH THE AREA OF THE RECTANGLE TO FIND THE VALUE OF X SUCH THAT THEIR AREAS WILL BE EQUAL

`4x + 16 = 3x + 18 \\ 4x - 3x = 18 - 16 \\ x = 2`

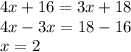
x=2

GOODLUCK!!