Answer:
The stone will be
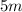 above the ground in
above the ground in

Step-by-step explanation:
As the stone is thrown vertically upward from ground with speed i.e.,
the initial velocity,
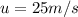 ,
,
the final velocity,
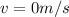 ,
,
acceleration due to gravity,
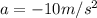 (upward motion)
(upward motion)
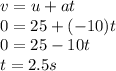
To calculate the height at which the stone reached above the ground we can use the below formula:
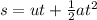

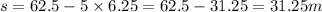
Now, the time taken by stone to reach
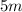 above the ground can be calculated using
above the ground can be calculated using
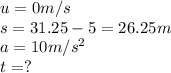
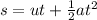
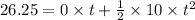



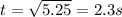
Thus, at
 the stone will reach
the stone will reach
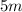 above the ground.
above the ground.