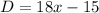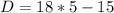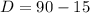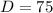Answer:
m<CAB = 54°
m<ABC = 21°
m<ACB = 105°
m<DCB = 75°
Explanation:
Part 1: Solve for x
The sum of the 3 interior angles of a triangle always equals 180°.
** Take note
Lets call m<CAB, angle A.
Lets call m<ABC, angle B.
Lets call m<ACB, angle C.
Lets call m<DCB, angle D.
So A + B + C = 180
Therefore we have
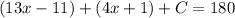
We have 1 more angle.
They gave us an exterior angle to help us find angle C.
A straight line is 180°.
They gave us one of 2 angles.
So
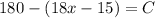
We can substitute
 for
for
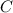 in our first equation.
in our first equation.
All together we have.
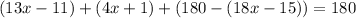

Now lets simplify and solve for
 .
.
Simplify each term.
Apply the distributive property.
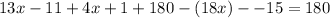
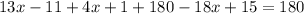
Simplify by adding like terms.
Add
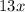 and
and
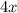 .
.
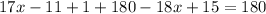
Subtract
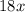 from
from
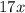 .
.

Simplify by adding numbers.
Add
 and
and
 .
.
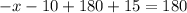
Add
 and
and
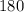 .
.
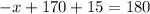
Add
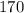 and
and
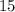 .
.
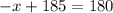
Move all terms not containing
 to the right side of the equation.
to the right side of the equation.
Subtract
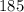 from both sides of the equation.
from both sides of the equation.
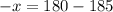
Subtract
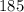 from
from
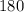
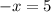
Divide each term by − 1 and simplify.


Part 2: Find the numerical value of each angle
We can now substitute 5 for x into the equations from the picture.
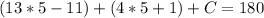
Angle A is
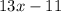
So A equals 54°
Angle B is
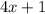
So B equals 21°
Remember
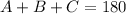 . We can solve for
. We can solve for
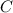 and we get.
and we get.
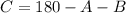

So C equals 105°
Remember a straight line is 180°.
We have 2 angles on the straight line. C and D
Therefore,

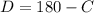
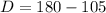
So D equals 75°
We can check. It gave us