Question

Help me do this …math

Answer 1

Explanation:

How to find inverse function:

Step 1: Write down equation.

`f(x) = 4 \sin(x) + 3`

Remeber Ruler notation that

f(x)=y so we replace y with f(x).

`y = 4 \sin(x) + 3`

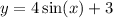
Next, we must isolate x so first we subtract 3.

`y - 3 = 4 \sin(x)`

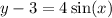
Divide both sides by 4.

`(y - 3)/(4) = \sin(x)`

`\sin {}^( - 1) ( (y - 3)/(4) ) = \sin {}^( - 1) ( \sin(x) )`

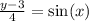
Remeber that sin^-1x and sin x are inverse functions so they will cancel out to x. So we get

`\sin {}^( - 1) ( (y - 3)/(4) ) = x`

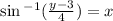
Swap x and y. So our inverse function is

`\sin {}^( - 1) ( (x - 3)/(4) ) = y`

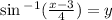
If you want another proof: Here's one,

Let plug an a x value for the orginal equation,

4 sin x+3. Let say that

`x = (\pi)/(2)`

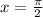
We then would get

`4 \sin( (\pi)/(2 ) ) + 3 = 4 * (1) + 3 = 4 + 3 = 7`

So when x=pi/2, y=7.

By definition of a inverse function, if we let 7 be our input, we should get pi/2. as a output.

So let see.

`\sin {}^( - 1) ( (7 - 3)/(4) ) = \sin {}^( - 1) ( (4)/(4) ) = \sin {}^( - 1) (1) = (\pi)/(2)`

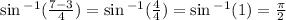
So this is the inverse function of 4 sin x+3.

1b. The range of f(x) is [-1,7).

We can use transformations to describe range.

We have

`f(x) = 4 \sin(x) + 3`

Parent function is

`\sin(x)`

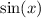
with a range of [-1,1].

We then vertical stretch by 4 so we get

`4 \sin(x)`

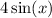
and our range will be

[-4,4].

Then we add a vertical shift of 3.

`4 \sin(x) + 3`

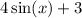
So our range of 4 sin x+3.

[-1,7].

1c. Domain of a inverse function is the range of the orginal function.

The range of f(x) is [-1,7) so the domain of f^-1(x) is [-1,7].

f(x) domain was restricted to -pi/2 to pi/2 so the range of f^-1(x) is [-pi/2, pi/2]