Question

Deon throws a ball into the air. The height, h, of the ball, in meters, at the time t seconds is modeled by the function h(t) = -5t + t + 4.

1. When will the ball hit the ground?

2. Will the ball reach a height of 5 meters?

Answer 1

1. 1 second.

2. No.

Explanation:

Given function:

`h(t)=-5t^2+t+4`

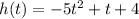
where:

• h is the height of the ball (in meters).
• t is the time (in seconds).

Question 1

The ball will hit the ground when the height is zero.

Substitute h = 0 into the given function and solve for t:

`\begin{aligned}h(t)&=0\\\implies -5t^2+t+4&=0\\-1(5t^2-t-4)&=0\\5t^2-t-4&=0\\5t^2-5t+4t-4&=0\\5t(t-1)+4(t-1)&=0\\(5t+4)(t-1)&=0\\\\5t+4&=0\implies t=-0.8\\t-1&=0 \implies t=1\end{aligned}`

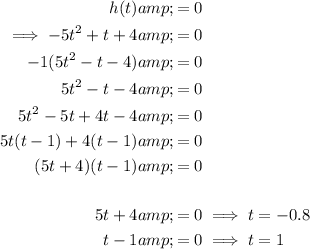
As t ≥ 0, t = 1 only.

Therefore, the ball will hit the ground after 1 second after it is thrown in the air.

Question 2

The x-coordinate of the vertex of a quadratic function is:

`\boxed{x=-(b)/(2a)}\quad \textsf{when $y=ax^2+bx+c$}.`

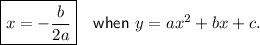
Therefore, the x-coordinate of the vertex of the given function is:

`\implies t=-(1)/(2(-5))=(1)/(10)=0.1`

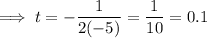
Substitute t = 0.1 into the function to find the maximum height of the ball:

`\implies h(0.1)=-5(0.1)^2+0.1+4=4.05`

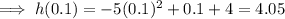
Therefore, the ball will not reach a height of 5 m, as the maximum height it can reach is 4.05 m, and 5 > 4.05.

Answer 2

• 1. After 1 second,
• 2. No.

Explanation:

Given function

• h(t) = - 5t² + t + 4

Solution

1) Ball hits the ground when:

• h(t) = 0, so

• - 5t² + t + 4 = 0
• 5t² - t - 4 = 0
• 5t² + 4t - 5t - 4 = 0
• t(5t + 4) - (5t + 4) = 0
• (t - 1)(5t + 4) = 0
• t - 1 = 0 or 5t + 4 = 0
• t = 1 or t = - 4/5

Solution is t = 1 and the second solution is discarded as negative.

The ball will hit the ground after 1 second.

2) Let's assume h(t) = 5, solve for t:

• - 5t² + t + 4 = 5
• - 5t² + t - 1 = 0
• 5t² - t + 1 = 0

• D = (-1)² - 4*5 = 1 - 20 = - 19

No solutions as the discriminant is negative, so the ball will not reach 5 meters.