Answer:
Mouse = 7
Hedgehog = 6
Owl = 4
Final equation = -2
Explanation:
Define the variables:
- Let x = mouse.
- Let y = hedgehog.
- Let z = owl.
The variables in the second equation are the same. Therefore, begin with this equation to determine the value that the mouse represents (x):

Following the order of operations, carry out the multiplication first:
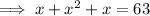
Add the like variables:

Subtract 63 from both sides:
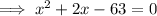
Factor and solve for x:

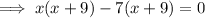
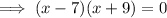
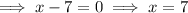
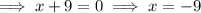
Therefore, the two possible values of the x are 7 and -9.
Evaluate the third equation where there are two variables:

Carry out the multiplication first:
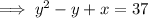
Subtract 37 from both sides:

As we have two possible values for x, substitute each value into the equation and solve for y.
Substitute x = 7 and solve for y:
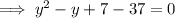
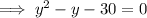
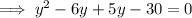
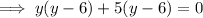
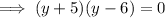
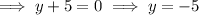

Substitute x = -9 and solve for y:
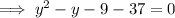
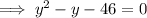
Using a calculator:
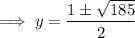
Assuming the numbers should be integers, we can discount x=-9 as it gives a non-integer value of y.
Therefore:
Evaluate the first equation where there are two variables:
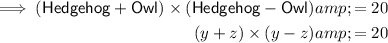
Simplify this equation and isolate z²:
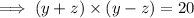

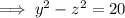
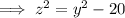
As we have two possible values for y, substitute each value and solve for z.
Substitute y = -5 and solve for z:
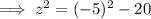
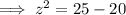
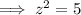
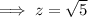
Substitute y = 6 and solve for z:
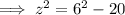

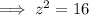

Again, assuming the numbers should be integers, we can discount y=-5 as it gives a non-integer value of z. Therefore:
Therefore, we have determined that:
- Mouse (x) = 7
- Hedgehog (y) = 6
- Owl (z) = 4
Substitute the found values into the fourth equation and solve:
