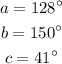Question

Find a, b and c. don’t be slow. show the equation and answer for all pls (:

Answer 1

`\begin{gathered} a=128^(\circ) \\ b=150^(\circ) \\ c=41^(\circ) \end{gathered}`

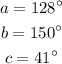
Step-by-step explanation:

Given the figure in the attached image.

We want to solve for a,b and c;

From the Geometry of circles, the inscribed angle is half the angle on the intercepted arc;

`\text{Inscribed angle=}(1)/(2)angle\text{ on the intercepted arc}`

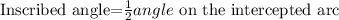
So, we have;

`\begin{gathered} c=(82^(\circ))/(2) \\ c=41^(\circ) \end{gathered}`

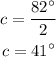
And;

`\begin{gathered} a=2(64^(\circ)) \\ a=128^(\circ) \end{gathered}`

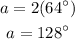
For b, the total angle of the circle circumference is 360 degrees;

`\begin{gathered} a+82^(\circ)+b=360^(\circ) \\ b=360^(\circ)-(82^(\circ)+a) \\ b=360^(\circ)-(82^(\circ)+128^(\circ)) \\ b=360^(\circ)-(210^(\circ)) \\ b=150^(\circ) \end{gathered}`

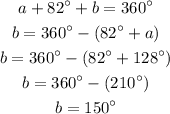
Therefore, we have;

`\begin{gathered} a=128^(\circ) \\ b=150^(\circ) \\ c=41^(\circ) \end{gathered}`