Write the pythagorean theorem for each one of the 3 right traingles:
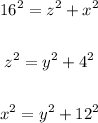
1. Solve x^2 in the first equation:
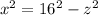
2. Solve y^2 in the second equation:
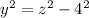
3. Substitute the x^2 and y^2 in the third equation by the values you get in the previous steps:
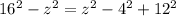
4. Solve z^2:
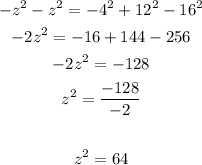
5. Use the value of z^2 to solve x and y:
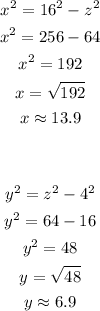
Then, the values of x and y are:x=13.9y=6.9