Question

Whucg expression is equivalent to (-4‐⁵)⁰?

Answer 1

Step 1

State a law of indices that can be used to simplify the expression

`(a^b)^c=(a)^(bc)`

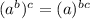
Step 2

Apply the law to solve the problem

`\begin{gathered} \text{From the law, in relation to the question} \\ a\text{ = -4} \\ b\text{ = -5} \\ c\text{ = 0} \\ \text{Therefore, after substitution, we would have} \\ (-4^(-5)_{})^0 \\ (-4)^(-5*0) \\ (-4)^0 \end{gathered}`

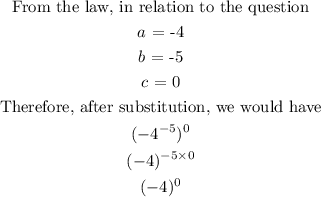
According to a law of indices, any number raised to the power of zero = 1

Therefore,

`(-4)^{0\text{ }}=1`

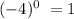
The right option, therefore, option A, 1