Answer:
1. (5, 0) is a solution to the inequality
2. (-2, 6) is not a solution to the inequality
Step-by-step explanation:
Given the inequality

We want to check if
1. (5, 0)
2. (-2, 6)
are solutions.
1. (5, 0)
Here, x = 5, y = 0
Insert these in the inequality, evaluate and see if the inequality is satisfied.

This is true, 0 is less than 23.
Hence, (5, 0) is a solution to the inequality
2. (-2, 6)
Here, x = -2, y = 6
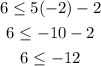
This is not true, 6 is neither less nor equal to -12
Hence, (-2, 6) is not a solution to the inequality.