Equation of the Parabola.
If the vertex of a parabola is located at the point (h, k), then the equation of the parabola is written as:

Where a is the leading coefficient. To find the coordinates of the vertex, given its equation, we use the 'square completion' technique.
We are given the equation:
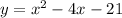
We need to transform this equation so it can be expressed like the general equation given above. Adding and subtracting 4:
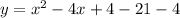
Rearranging:
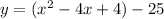
Factoring:
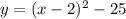
The vertex of the parabola is located at (2, -25).
To find the x-intercepts, we set y=0 and solve the equation:
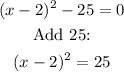
Taking the square root (it has two signs):

Solving for x, we get two possible answers:
x = 5 + 2 = 7
x = -5 + 2 = -3
X-inercepts: -3, 7