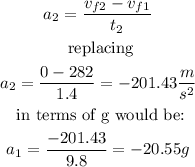ANSWER:
a. 5.75g
b. -20.55g
Explanation:
We have the following information from the statement:
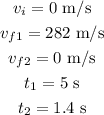
To calculate the acceleration during the first part of the motion it would be:
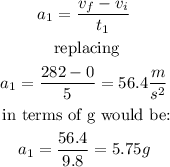
To calculate the acceleration during the second part of the movement it would be: