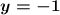To solve the exercise, we can first find the slope of the line that passes through the given points. For this, we can use the following formula:
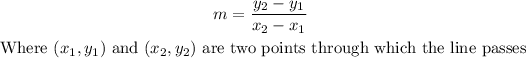
Then, we have:

As you can see, the line has a slope of zero, that is, it is a horizontal line.
The equation of a horizontal line is:

Where y₁ coincides with b, the y-intercept of the line.
Therefore, the equation in its slope-intercept form of the line containing the given points is: