Question

Just uhh… it’s a lot, I’ll try to do this by myself.

Answer 1

`\textsf{(a)} \quad -2x-4`

`\textsf{(b)} \quad 2x+5`

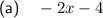
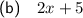
(c) Not equivalent.

`\textsf{(d)} \quad 3x^2-24x+48`

`\textsf{(e)} \quad 9x^2-72x+144`

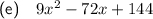
(f) Not equivalent.

Explanation:

Equivalent expressions are expressions that simplify to the same expression.

Part (a)

`\begin{aligned}&\textsf{Add 3 to $x$}: & \quad x+3\\&\textsf{Subtract the result from $1$}: & \quad 1-(x+3)\\&\textsf{Double}: & \quad 2[1-(x+3)]\\&\textsf{Expand}: & \quad 2[1-x-3]\\&\textsf{Simplify}:&2[-x-2]\\&& -2x-4\end{aligned}`

Part (b)

`\begin{aligned}&\textsf{Add 3 to $x$}: & \quad x+3\\&\textsf{Double}: & \quad 2(x+3)\\&\textsf{Subtract $1$ from the result}: & \quad 2(x+3)-1\\&\textsf{Expand}: & 2x+6-1\\&\textsf{Simplify}:&2x+5\end{aligned}`

Part (c)

The expressions are not equivalent.

The coefficients of the x-variables are the negatives of one another, and the constants are different numbers.

Part (d)

`\begin{aligned}&\textsf{Subtract 4 from $x$}: & \quad x-4\\&\textsf{Square the result}: & \quad (x-4)^2\\&\textsf{Triple}: & \quad 3(x-4)^2\\&\textsf{Expand}: & \quad 3(x^2-8x+16)\\&\textsf{Simplify}:& 3x^2-24x+48\end{aligned}`

Part (e)

`\begin{aligned}&\textsf{Subtract 4 from $x$}: & \quad x-4\\&\textsf{Triple the result}: & \quad 3(x-4)\\&\textsf{Square}: & \quad [3(x-4)]^2\\&\textsf{Expand}: & \quad [3x-12]^2\\&\textsf{Simplify}:& 9x^2-72x+144\end{aligned}`

Part (f)

The expressions are not equivalent.

The coefficients the second equation are three times the coefficients of the first equation.