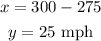Answer:
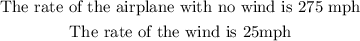
Explanation:
Speed is represented by the relation of the distance and time, therefore for the speed against the wind;
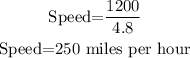
Therefore, let x be the wind speed.
let y be the airplane speed at no wind.
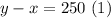
Now, the speed with the wind:
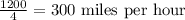
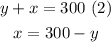
Hence, use the method of substitution to solve the system of equations. Substitute (2) into (1):
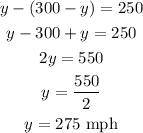
Knowing the value of the plane with no wind. Substitute y into (2) to find the speed of the wind: