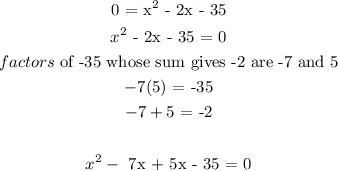Question

What are the vertex and x-intercepts of the graph of the function given below?

Answer 1

Answer:

Vertex: (1, -36); intercepts: x = 7, -5 (option D)

Step-by-step explanation:

Given:

`y\text{ = x}^2\text{ - 2x - 35}`

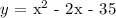
To find:

the vertex and the x-intercepts

i) Vertex is given as (h, k). To determine the vertex, we will apply the formula:

`\begin{gathered} h\text{ = }(-b)/(2a) \\ k\text{ = f\lparen h\rparen} \\ from\text{ the given equation:} \\ a\text{ = 1, b = -2 c = -35} \\ \\ h\text{ = }(-(-2))/(2(1))\text{ = 2/2} \\ h\text{ = 1} \\ \\ k\text{ = f\lparen h\rparen} \\ We\text{ will substitute the value of h with x in the given equation} \\ y\text{ =1}^2\text{ - 2\lparen1\rparen - 35} \\ y\text{ = -36} \\ k\text{ = -36} \end{gathered}`

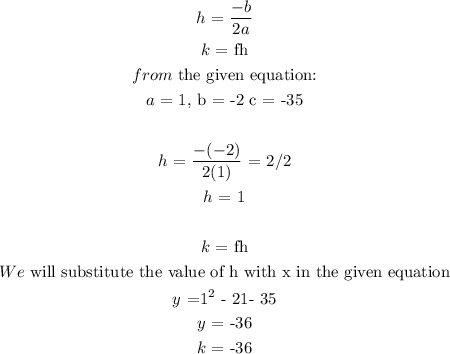
Vertex (h, k): (1, -36)

ii) x-intercept is the value of x when y = 0. To determine x-intercept, we will substitute y with 0. Then solve for x

`\begin{gathered} 0\text{ = x}^2\text{ - 2x - 35} \\ x^2\text{ - 2x - 35 = 0} \\ factors\text{ of -35 whose sum gives -2 are -7 and 5} \\ -7(5)\text{ = -35} \\ -7+5\text{ = -2} \\ \\ x^2-\text{ 7x + 5x - 35 = 0} \end{gathered}`
`\begin{gathered} factorise: \\ x(x\text{ - 7\rparen + 5\lparen x - 7\rparen = 0} \\ (x\text{ + 5\rparen\lparen x - 7\rparen = 0} \\ x\text{ + 5 = 0 or x - 7 = 0} \\ x\text{ = -5 or x = 7} \\ The\text{ x-intercepts are x = 7, -5} \end{gathered}`