Question

A cylinder has a radius of 2.5 meters. Its volume is 757 cubic meters. Find the cylinders height. Round your answer to the nearest tenth.

Answer 1

The information we have about the cylinder is:

The radius

`r=2.5m`

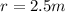
The volume

`V=757m^3`

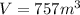
To find the height, we have to use the general formula for the volume of a cylinder:

`V=\pi r^2h`

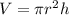
Where h is the height of the cylinder.

The first step will be to solve for h in the previous formula by dividing both sides by πr^2:

`(V)/(\pi r^2)=h`

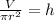
The second step will be to substitute the values of the volume and the radius:

`(757m^3)/(\pi(2.5m)^2)=h`

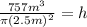
We also substitute the value of pi:

`\pi=3.1416`

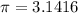
And we get:

`(757m^3)/((3.1416)(2.5m)^2)=h`

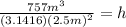
The third step is to solve the operations:

`(757m^3)/((3.1416)(6.25m^2))=h`
`(757m^3)/(19.635m^2)=h`
`38.55m=h`

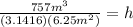
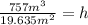
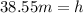
The height of the cylinder is 38.55m

Rounding to the nearest tenth: 38.6m

Answer: 38.6m