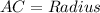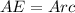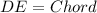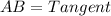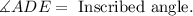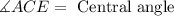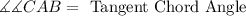1 Answer

Jyo Fanidam · Answer 1 · 2023-11-16T07:53:55+0000

Given:

A circle with a center at C.

Required:

We need to find the names of the given parts.

Step-by-step explanation:

Recall that radius is a line segment extending from the center of a circle to the circumference.

Line segment AC extends from the center C of a circle to the circumference.

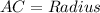
Recall that the arc of a circle is defined as the part of the circumference of a circle.

AE is the part of the circumference of a circle.

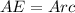
Recall that a straight line segment joins and is included between two points on a circle.

D and E are two points on a circle.

A straight line DE line segment joins and is included between two points D and E on a circle.

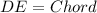
Recall that meeting a curve or surface in a single point if a sufficiently small interval is considered a straight line tangent to a curve.

AB is tangent.

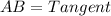
Recall that an inscribed angle is an angle with its vertex "on" the circle, formed by two intersecting chords.

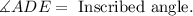
$\measuredangle ADE=\text{ Inscribed angle.}$

Recall that a central angle is an angle formed by two radii with the vertex at the center of the circle.

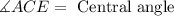
$\measuredangle ACE=\text{ Central angle}$

Recall that an angle formed by an intersecting tangent and chord has its vertex "on" the circle.

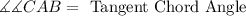
$\measuredangle\measuredangle CAB=\text{ Tangent Chord Angle}$

Final answer:

$\measuredangle ADE=\text{ Inscribed angle.}$

$\measuredangle ACE=\text{ Central angle}$

$\measuredangle\measuredangle CAB=\text{ Tangent Chord Angle}$

Please log in or register to add a comment.